Finite state machines
Hybrid Meetup #43 took place 2024-05-28 at Gridfuse, Hauptpost Leipzig. We had a great presentation about a lightweight (~200 LOC), open source state machine library written in Go: ekstatic — presentation slides (PDF)
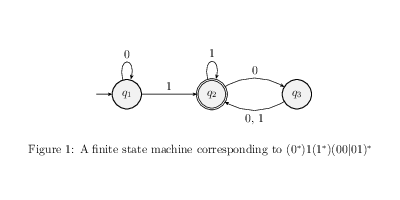
The use case in the context of RAIDA is the modelling of workflows, composed of a number of steps (and the loose coupling of business logic with state transistions). The library is flexible, but the limits of the Go type system require to resort to any (which will defer some type checks to runtime).
For convenience, the predeclared type
anyis an alias for the empty interface. [Go 1.18]
The library is open source at Metamogul/ekstatic, and contains some examples as well. Thanks again, Jan for the insights, and Gridfuse for hosting another Leipzig Gophers event.
Misc
- code generation may improve type safety of a generic FSM Go implementation, similar to sqlc and other libraries
- railway oriented control flow, reminding one of The happy path is left-aligned
- Rust std::result in combination with the ? operator makes working with errors easier; there are libraries in Go, like alexthomas/types, that try emulate that; or even language proposals (declined at the time)
- another, albeit much more extensive library for workflows (or durable execution) is temporal, which has a go client as well
- contracts has been tried in various places in software systems, e.g. design by contract, or PACT for REST testing
- GraphQL is a nice alternative to representional state transfer (REST); libraries: gqlgen for servers, gqlgenc for clients
- Rob Pike on state machines, 12 years ago: Lexical Scanning in Go - Rob Pike, What is a state? [13:45]
Monads
A finite state machine consists of states and state transitions; implementationwise, a state may be any type, but at the same time we would benefit from marking a type as a state, hence unifying different actions. A variant type could be a solution, but Go does not support variant types (albeit interfaces and type switches allow for some unification).
In essence, we would like chainable computation, or workflow composition, which is reminding of monads.
- the morning paper: Monads for functional programming
- A monad is just a monoid in the category of endofunctors, what’s the problem?
Sidenote: For Leibniz, monads were the essential substance (1714), which has no parts and is therefore indivisible. They also were windowless, or immutable.
The Monads have no windows, through which anything could come in or go out.
A few years earlier, in 1703, Leibniz recognized something else essential: the binary number system.
But reckoning by twos, that is, by 0 and 1, as compensation for its length, is the most fundamental way of reckoning for science, and offers up new discoveries, which are then found to be useful, even for the practice of numbers and especially for geometry. The reason for this is that, as numbers are reduced to the simplest principles, like 0 and 1, a wonderful order is apparent throughout.
